Multifractals in ecology using R
tags: real-examples math equations
Description/Summary
Disclaimer This post is from the link posted by GitHub user lsaravia in this comment. All credit for this post goes to the original author. Multifractals # Many natural systems cannot be characterized by a single number such as the fractal dimension. Instead an infinite spectrum of dimensions must be introduced. Multifractal definition # Consider a given object \(\Omega\), its multifractal nature is practically determined by covering the system with a set of boxes \(\{B_i( r)\}\) with \((i=1,…, N( r))\) of side length \(r\)
Content
- Disclaimer
- This post is from the link posted by GitHub user lsaravia in this comment. All credit for this post goes to the original author.

Multifractals #
-
Many natural systems cannot be characterized by a single number such as the fractal dimension. Instead an infinite spectrum of dimensions must be introduced.

Multifractal definition #
-
Consider a given object \(\Omega\), its multifractal nature is practically determined by covering the system with a set of boxes \(\{B_i( r)\}\) with \((i=1,…, N( r))\) of side length \(r\)
-
These boxes are nonoverlaping and such that
\[\Omega = \bigcup_{i=1}^{N( r)} B_i( r)\]
This is the box-counting method but now a measure \(\mu(B_n)\) for each box is computed. This measure corresponds to the total population or biomass contained in \(B_n\), in general will scale as:
\[\mu(B_n) \propto r^\alpha\]
Box counting #
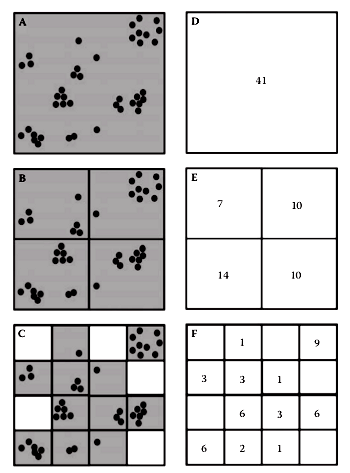
The generalized dimensions #
-
The fractal dimension \(D\) already defined is actually one of an infinite spectrum of so-called correlation dimension of order \(q\) or also called Renyi entropies.
\[D_q = \lim_{r \to 0} \frac{1}{q-1}\frac{log \left[ \sum_{i=1}^{N( r)}p_i^q \right]}{\log r}\]
where \(p_i=\mu(B_i)\) and a normalization is assumed:
\[\sum_{i=1}^{N( r)}p_i=1\]
-
For \(q=0\) we have the familiar definition of fractal dimension. To see this we replace \(q=0\)
\[D_0 = -\lim_{r \to 0}\frac{N( r)}{\log r}\]
Generalized dimensions 1 #
-
It can be shown that the inequality \(D_q’ \leq D_q\) holds for \(q’ \geq q\)
-
The sum
\[M_q( r) = \sum_{i=1}^{N( r)}[\mu(B_i( r))]^q = \sum_{i=1}^{N( r)}p_i^q\]
is the so-called moment or partition function of order \(q\).
-
Varying q allows to measure the non-homogeneity of the pattern. The moments with larger \(q\) will be dominated by the densest boxes. For \(q<0\) will come from small \(p_i\)’s.
-
Alternatively we can think that for \(q>0\), \(D_q\) reflects the scaling of the large fluctuations and strong singularities. In contrast, for \(q<0\), \(D_q\) reflects the scaling of the small fluctuations and weak singularities.
Exercise #
-
Calculate the partition function for the center and lower images of the figure:

Two important dimensions #
-
Two particular cases are \(q=1\) and \(q=2\). The dimension for \(q=1\) is the Shannon entropy or also called by ecologist the Shannon’s index of diversity.
\[D_1 = -\lim_{r \to 0}\sum_{i=1}^{N( r)} p_i \log p_i\]
and the second is the so-called correlation dimension:
\[D_2 = -\lim_{r \to 0} \frac{\log \left[ \sum_{i=1}^{N( r)} p_i^2 \right]}{\log r} \]
the numerator is the log of the Simpson index.
Application #
-
Salinity stress in the cladoceran Daphniopsis Australis. Behavioral experiments were conducted on individual males, and their successive displacements analyzed using the generalized dimension function \(D_q\) and the mass exponent function \(\tau_q\)
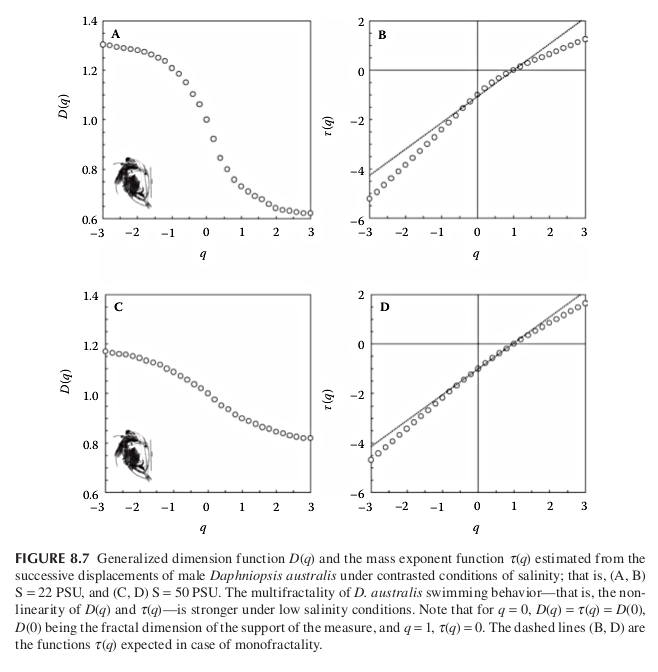
both functions indicate that the successive displacements of male D. australis have weaker multifractal properties. This is consistent with and generalizes previous results showing a decrease in the complexity of behavioral sequences under stressful conditions for a range of organisms.
-
A shift between multifractal and fractal properties or a change in multifractal properties, in animal behavior is then suggested as a potential diagnostic tool to assess animal stress levels and health.
Mass exponent and Hurst exponent #
-
The same information contained in the generalized dimensions can be expressed using mass exponents:
\[M_q( r) \propto r^{-\tau_q}\]
This is the scaling of the partition function. For monofractals \(\tau_q\) is linear and related to the Hurst exponent:
\[\tau_q = q H - 1\]
For multifractals we have
\[\tau_q = (q -1) D_q\]
Note that for \(q=0\), \(D_q = \tau_q\) and for \(q=1\), \(\tau_q=0\)
Paper #
- Kellner JR, Asner GP (2009) Convergent structural responses of tropical forests to diverse disturbance regimes. Ecology Letters 12: 887–897. https://doi.org/10.1111/j.1461-0248.2009.01345.x.
Page (Debug)
| Page Variable | Value | |
|---|---|---|
| Name | "Multifractals in ecology using R" | |
| Title | "Multifractals in ecology using R" | |
| ResourceType | "page" | |
| Kind | "page" | |
| Section | "real-examples" | |
| Draft | false | |
| Type | "real-examples" | |
| Layout | "" | |
| Permalink | "https://ox-hugo.scripter.co/test/real-examples/multifractals-in-ecology-using-r/" | |
| RelPermalink | "/real-examples/multifractals-in-ecology-using-r/" | |
| Data |
| |
| NextPage | 神经网络基础 | |
| PrevPage | Date + Time (behind UTC) | |
| NextInSection | 神经网络基础 | |
| PrevInSection | None |
Page Params (Debug)
| Key | Type | Value |
|---|---|---|
| author | []string | "Leonardo A. Saravia" |
| date | time.Time | 2017-11-28 10:48:00 -0500 -0500 |
| draft | bool | false |
| iscjklanguage | bool | false |
| lastmod | time.Time | 2021-10-21 21:31:32 -0400 -0400 |
| publishdate | time.Time | 2017-11-28 10:48:00 -0500 -0500 |
| source | string | "https://github.com/lsaravia/MultifractalsInR/blob/master/Curso3.md" |
| tags | []string | "real-examples" "math" "equations" |
| title | string | "Multifractals in ecology using R" |
File Object (Debug)
| FileInfo Variable | Value |
|---|---|
| UniqueID | "052682e6df8b2eb0b7895545d30daff6" |
| BaseFileName | "multifractals-in-ecology-using-r" |
| TranslationBaseName | "multifractals-in-ecology-using-r" |
| Lang | "en" |
| Section | "real-examples" |
| LogicalName | "multifractals-in-ecology-using-r.md" |
| Dir | "real-examples/" |
| Ext | "md" |
| Path | "real-examples/multifractals-in-ecology-using-r.md" |